IPL Auction Simulator 

This project attempts to build a small-scale simulation of what is commonly referred to as a pre-season  mini-auction for the IPL. In addition, we incorporate Reinforcement Learning to enable the teams to make reasonably intelligent decisions, on who to bid for and for what price.  

Aim

As mentioned previously, this project aims to build a basic IPL auction simulator, with teams making intelligent decisions on which players to choose. The detailed features of this are as follows:

• In order to model the IPL auction process appropriately, set up a Markov Decision Process (MDP), defining appropriate states of the auction/team, actions that the teams in the auction can take and an appropriate reward system, to enable the RL-agent to learn from the experience effectively.  
• Based on the MDP setup, choose an appropriate RL algorithm (especially based on the *rewards*) that not only enables learning, but also fits into IPL auction simulator system the best.  
• Build an IPL mini-auction simulator: a socket client-server based system, wherein the server acts as the auctioneer, and the different clients emulate the different teams in the auction.
• Integrate the simulator with a high-level UI, to enable users to see the ongoing auction-simulation.

Prerequisites

We will now introduce some preliminaries, to help better understand the workflow of our project.  

About the IPL auction

The Indian Premier League is a global-level T20 cricket league that is annually held in India. There are 10 teams(2024), which each have a min/max of 18/25 players. In order to help slightly balance out teams and introduce rising cricketers into the IPL (both domestic and foreign), the annual IPL mini-auction is conducted (as opposed to a mega-auction, which is beyond the scope of this project).

In the mini-auction, teams have an already semi-built team, and try to gain a few extra players to fill in specific requirements, like requiring some spinners, need a finisher/opener, etc. Teams are given a common *purse*, which is reduced based on the already retained players. Utilizing strategies and careful usage of the remaining purse, teams will attempt to maximize their overall team quality, without exceeding their purse.

  
MDP-based Reinforcement Learning

In classical RL, the major mathematical modelling is based on a Markov Decision Process (MDP). Formally, an MDP is a 4-tuple

(S, A_s, P_a, R_a), wherein:

• S is set of all possible states (typical terminology: s - current states, s' - next state)
• A_s is the set of all actions possible from the current state \(​ s \epsilon S ​\) (typical terminology: s - current action, s' - next action)
• P_a is the probability distribution function (involves s and s'), which shows Probability of landing in s', having been in s and committing a*.
• R_a is the reward function (involves s and s'), which returns Reward received from the environment for landing in s', having been in s and committing a.

The overall MDP is visually represented as the below cycle-diagram:

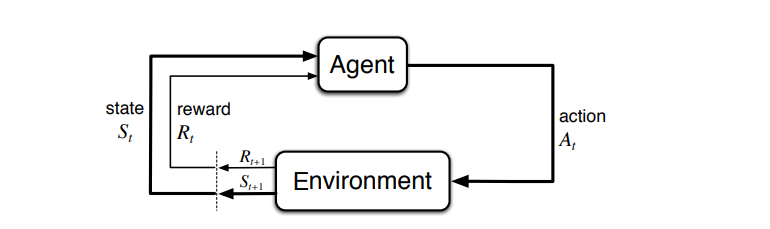
  Once the 4-tuple(S, A_s, P_a , R_a) is setup for a problem, our objective is to maximize the expected reward that is obtained in a run-through of the problem. In classical RL, this is done by estimating the values of state-action (s, a) pairs, denoted Q(s, a). Formally, Q is the expected discounted reward obtained in a single iteration of the problem (an episode). This is aptly formulated as follows  

\(Q^\pi(s, a) = {\bf E}_{\pi} [ \sum_{k=0}^{\infty} \gamma^k r_{t+k+1} | s_{t} = s, a_{t} = a ]\) (1)

In the literature, optimal values for Q(s, a) are obtained using the Bellman equation:

\(Q^*(s, a) = R(s, a) + \gamma \sum_{s' \in S} P_{ss'}(a) \max_{a' \in A(s')} Q^*(s', a') \) (2)

Also, based on these optimal \(Q^*(s,a)\) values, a policy \(\pi\) is determined as follows:

\(\pi^*(s) = \arg\max_a q^{\pi}(s,a) \) (3)

In reality, we would never have access to \(P_{ss'}\), since this is an intrinsic property of the environment, which is likely only partially/never revealed. In addition, the above optimal solution is only exactly attainable, in the limit of infinity. Hence, we turn to some of the existing value-based approximation algorithms, to achieve reasonable optimality, in finite time.

Monte-Carlo RL

Monte-Carlo (MC) for Reinforcement Learning is an important value-based model free algorithm, whose specialty lies in the fact that the Q-values are updated at the end of an episode. This way, (1) is as closely emulated is possible. Furthermore, one immediate advantage of MC is that it can distribute the discounted reward to all the states that occur in an episode. This is particularly useful in scarce-reward scenarios (when the reward is just 0/1), or when the reward is given at the end of the episode (ex: 0 or 1 for losing or winning a round of Blackjack). An overall view of the algorithm is shown below:

To see an example tutorial of implementing the above algorithm in a Gymnasium environment (as show below), refer our repository:

Methodology and Design

Modelling the IPL mini-auction

We formalized the following flow of the auction, heavily influenced by the model followed in the real IPL mini-auction. It consists of two main stages for each player:

1. The initial bid

Each player is designated a certain base price and is put up on auction, open to all teams. Any teams that are interested in the player at the given price place their bids on the player.

• If no team is interested, the player goes unsold.
• If only one team is interested, the player is sold to that team at the base price.
• If more than one team is interested, two of the interested teams are chosen on random, and move on to the next stage.

2. The two-team bidding

The two teams chosen at random from the previous stage go head-to-head, bidding a higher price for the current player at each step. This continues until any one of the two teams back out from the bid. The new price of the player is set to the final bid of this stage.

At this point, the remaining teams from the previous stage are again requested to submit their bids for the player at the new price. If any teams are interested in this, one team is again chosen at random and stage 2 is repeated again between the current owner of the player and the chosen team.

Data Collection

The data required for the RL algorithm were various stats related to batting and bowling . We initially tried to scrape the required  data directly from the Cricinfo website using pandas querying, which couldn't be done due to the anti scraping mechanism used by the website. Hence, we tried an alternate option of downloading a dataset from  Kaggle, and then by using Pandas library as well as Numpy library, was able to organize data and store it in a .CSV file format.

The data in the dataset contained ball by ball info of all the IPL season. The goal was to extract statistics such as aggregate runs, strike rate, wickets taken, etc. which could then be used by the bots to determine whether to bid for a particular player or not, as well as aiding in evaluating the team built by the bot in order to give the reward. The data was formatted by grouping data wrt a player's name and then adding or counting the elements of a particular column based on the stat to be calculated, and then storing it in their respective column. We used Pandas library to read and write data from and to the .CSV file whereas used Numpy to manipulate the rows and columns of the data.
  

System Design  

The IPL auction simulator project (inspired from the above) consists of 3 parts: the socket server, acting as the auctioneer, coupled with a database to store and retrieve data; the RL model/algorithm which acts as the team, making decisions during the auction process; and the frontend UI, to showcase the process taking place in a user-friendly format The further specifics are discussed below.

RL Agent Design  

To keep track of the entire player-bidding flow, plus integrating the crucial RL algorithm itself, we split the functionalities into several classes. This helps make our design more robust, and creates a design to allow improvement in the future.

Player
Keeps track of player's quality/rating, current price, and role they would play in the team.

Team
To keep track of the team being built during the auction, maintain list of Players, and also provide a crucial method for determining the current team rating, to provide the agent with another dimension of learning.

SA Manager
This is a unique manner of implementing the all of the RL agent logic: defining state & action spaces, determining current state, based on player announced by auctioneer, the optimal action to be taken at that moment in the auction, and the associated reward to bundle all of it together. These aspects are implemented as methods that can be easily and discretely called as an API for the Bot class, unlike normal testing in standard environments, say like in Gymnasium (all the logic is fluid and together, in a continuous loop, since the agent is primarily in control of the environment reacting).

Bot
The highest layer of abstraction that ties the previous classes into the bot that represents the IPL team. They record how the IPL auction goes (i.e. record the episode) and have a method to train its *agent logic*. Regardless, only the ==optimal_action== method is exposed to the system, to provide a clean and simple interface to the system. This optimal_action method calls all the important logic developed above, and ultimately decides the current best move for the team bot.

Rewards
The major way that any RL agent learns is through the rewards. And, in the complex environment that is the IPL auction, a reward system with different dimensions and aspects is useful. We use two reward functions: a step and episodic reward function, to assign appropriate credit to all the states passed through. Both these functions take into account several factors:

• Team balance (between batters, bowlers, all-rounders, etc.)

• Potential improvement, if a team acquires a player

• Purse remaining for next season auction

• Number of players is in the 18-25 range

• Overall quality of the team.

These reward are used, in a discounted manner, using hyperparameter \(\gamma\), to give appropriate importance to both immediate and delayed/future reward.

Creating an Auctioneer server to conduct the auction  

The following technologies were used in the design of the auction server:  

Web Sockets

Since the problem statement involves a multi-team auction, a centralized auction server is necessary to enable effective communication between the agents. As this is a real-time application, we decided to use `WebSocket` to design the server. To allow simple structuring of the server and enable use of an event-driven model, we used `socket.io` framework for the socket-server.

After deciding upon the flow of the auction, appropriate `socket.io` events were made for the process, as documented [here](./server/socket_events.md). These events are used both by the server and the client (agent or team) to communicate between each other during the process of the auction.

MongoDB

During the auction, it is necessary to also store the data of the players chosen by each team in a permanent database. Since the structure of this data might not be strongly defined, we chose to use the document-oriented database `MongoDB`, to store this data.

Redis

Since the pace of the auction will be very fast (as it consists of bots), the server has to handle the requests to it with very little latency, and at a very high frequency. MongoDB, while performant, does not match this level of concurrency requirement. This calls for a secondary cache database, such as `Redis`. Redis is able to handle huge throughput and provide ultra-low latency as it stores the data in main memory instead of on disk. This data will then sequentially be written into the MongoDB database, ensuring presistence of data.

Kafka

Even though the final teams are stored in the MongoDB database with Redis as a cache layer, the individual actions by each team, and each step in the auction, go unrecorded. To provide the user with full data about the proceedings of the auction, these actions need to be recorded. This is the perfect use case for a message-queue platform such as `Kafka`. This allows "messages" to be stored in sequence, and replayed at a later time. This enables a full replay of the auction process.

HTTP API

To allow the front-end application to access data from the MongoDB database, a HTTP API is used, built in NodeJS using ExpressJS. This API has routes to get information about the players drafted by each team, to display the same in the UI.

The Frontend

The front-end application, built using ReactJS and TailwindCSS, provides an interface for the whole project. During an auction, it shows the current player under auction, and the current status of the auction process. This data is retrieved using the [Kafka message queue](#kafka), which stores the actions taking place in the auction.

After the completion of the auction, the user will be able to view the final team composition of all the teams that took part in the auction. This data, present in the MongoDB database, is accessed with the help of the [HTTP API](#http-api) and is displayed in a user-friendly format.

Conclusions

• We explored the problem statement and data available on the matter. The data was aggregated to get useful information about each player, to evaluate the strength and value of each player.
• An MDP was formulated with appropriate states, actions and rewards, and we concluded that On Policy Monte-Carlo RL would be most suited for the problem statement and the decided environment.
• To test the bots in a multi-agent environment, a socket server was used to mimic the auctioneer-team system of an actual IPL auction. This server was designed considering the requirements of the application, using cache databases and message queues to achieve necessary performance.
• Several variations were made to the RL model to arrive at a satisfactory solution to the problem. Extensive training was used to improve it's accuracy in decision making.
• A front-end interface was made to showcase the results of the auction in a user-friendly format, displaying the final composition of the teams that were drafted by the bots.

References

• https://www.iplt20.com/
• https://en.wikipedia.org/wiki/Indian_Premier_League
• https://en.wikipedia.org/wiki/Markov_decision_process
• http://incompleteideas.net/book/the-book-2nd.html
• https://www.youtube.com/@Mutual_Information
• https://gymnasium.farama.org/